e-Funktion

Wir wollen uns hier die e-Funktion etwas genauer anschauen. Sie gehört zu den Exponentialfunktionen – nicht zu verwechseln mit den Potenzfunktionen wie y = x^2. Bei Potenzfunktionen steht die Variable (x) in der Basis, während bei den Exponentialfunktionen, also auch der e-Funktion die Variable im Exponenten steht.

Was genau ist die e-Funktion?

Bei der e-Funktion handelt es sich um eine Exponentialfunktion mit der Basis e. Die Funktionsgleichung der e-Funktion lautet f(x) = e^x. Dabei steht e für die Eulersche Zahl mit dem folgenden Wert:

e = 2,718182…

Benannt wurde die Eulersche Zahl nach dem Mathematiker Leonhard Euler. Schon im Jahr 1748 fand er heraus, dass die Eulersche Zahl den Grenzwert der unendlichen Reihe darstellt. In Deinem Taschenrechner ist die Zahl e als Konstante eingespeichert, was Dir die Berechnungen erleichtert.

Graphen der e-Funktion ermitteln

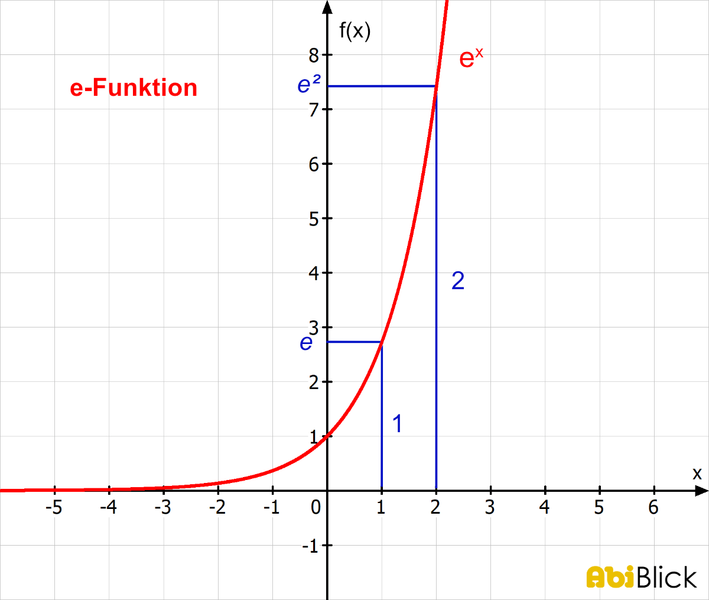
Um die e-Funktion besser zu verstehen und ihre Eigenschaften abzuleiten, ist es empfehlenswert, zunächst den Graphen der Funktion zu zeichnen. Dafür kannst Du mit dem Taschenrechner ein paar Funktionswerte berechnen. Runde die Ergebnisse auf zwei Stellen nach dem Komma. Das ist ausreichend, um einen Graphen zu zeichnen.

f(-2) = e^-2 = 0,14
f(-1,5) = e^-1,5 = 0,22
f(-1) = e^-1 = 0,37
f(-0,5) = e^-0,5 = 0,61
f(0) = e^0 = 1
f(0,5) = e^0,5 = 1,65
f(1) = e^1 = 2,72
f(1,5) = e^1,5 = 4,48
f(2) = e^2 = 7,39

Zeichne nun die berechneten Funktionswerte an den jeweiligen x-Werten im Koordinatendiagramm ein, um den Graphen der Funktion f(x) = e^x zu erhalten.

Eigenschaften aus dem Graphen ableiten

Wenn Du Dir den Graphen der e-Funktion genauer anschaust, kannst Du daraus die wichtigsten Eigenschaften ableiten:

Der Graph der Funktion verläuft komplett oberhalb der x-Achse. Daraus ergibt sich die Wertemenge der e-Funktion, nämlich W = R+.
Der Graph der e-Funktion nähert sich der x-Achse an. Demzufolge ist die x-Achse gleichzeitig die waagerechte Asymptote dieser Exponentialfunktion.
Im Punkt (0|1) wird die y-Achse vom Graphen der e-Funktion geschnitten, weil e^0 = 1 laut Potenzgesetz gilt.
Die x-Achse wird hingegen nicht vom Graphen der e-Funktion geschnitten, sodass diese Funktion keine Nullstellen hat.
Der Graph der e-Funktion ist streng monoton steigend. Das bedeutet, je größer x, desto größer ist auch y.

Vielleicht kennst Du bereits die ln-Funktion? Dann dürfte Dir aufgefallen sein, dass die e-Funktion genau die entgegengesetzten Eigenschaften der ln-Funktion besitzt. Das hat auch einen guten Grund, denn die ln-Funktion ist die Umkehrfunktion der e-Funktion.

Ableitung und Umkehrfunktion der e-Funktion

Die Ableitung der e-Funktion stellt einen Sonderfall dar, denn: Die Ableitung entspricht der Funktion selbst. Das heißt:

f(x) = f‘(x) = f‘‘(x) = …

Die Stammfunktion der e-Funktion bildet ebenfalls wieder die e-Funktion. Es gilt also:

Ableitung: f'(x) = e^x
Stammfunktion: F(x) = e^x

Aber warum gilt das für die e-Funktion? Hierfür schauen wir uns die allgemeine Ableitung von Exponentialfunktionen an. Diese lautet:

f(x) = a^x -> f‘(x) = a^x! * ln(a)

Sofern wir das auf die e-Funktion f(x) = e^x anwenden, ergibt sich:

f‘(x) = (e^x)‘ = e^x! * ln(e) = e^x! * 1 = e^x

Du siehst, es liegt also daran, dass ln(e) = 1 ergibt, dass die Ableitung und die Umkehrfunktion der e-Funktion wieder die Funktion selbst ist.