Geometrische Figuren sind "kongruent", wenn sie hinsichtlich FOrm und Flächeninhalt vollkommen gleich (deckungsgleich) sind. Hierbei können die Figuren zueinander verschoben,oder gespiegelt sein.
Kongruente Figuren
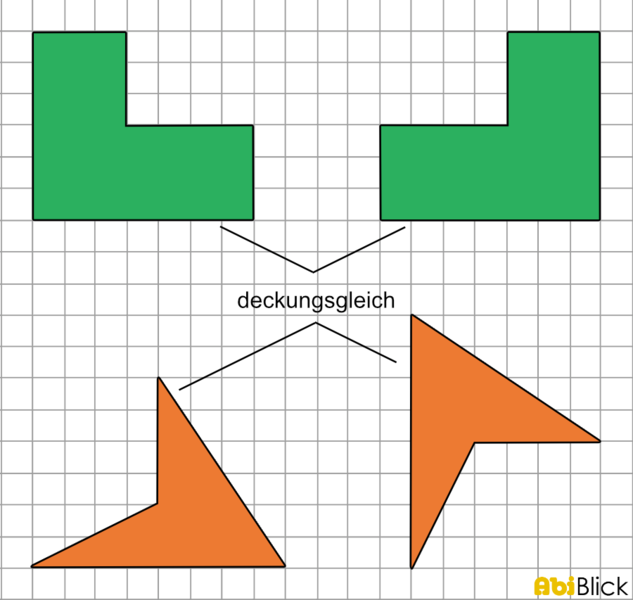
Im Bild siehst du jeweils zwei kongruente Figuren. Diese sind trotz Spiegelung oder Verschiebung exakte Kopien voneinander. Umgangssprachlich würde man einfach sagen die Figuren sind "gleich". Mathematisch spricht man jedoch von "kongruenten" Figuren. Figuren sind nur dann kongruent, wenn Seitenlängen und Innenwinkel übereinstimmen.
Kongruente Figuren erhält man durch:
- Verschiebung
- Drehung
- Spiegelung
Kongruente Dreiecke
Eine beliebte Matheaufgabe beginnt mit folgendem Satz: "Untersuche die beiden Dreiecke hinsichtlich Kongruenz...". Es gibt vier sogenannte Kongruenzsätze, anhand derer untersucht werden kann ob zwei Dreiecke kongruent sind. Alle vier Kongruenzsätze prüfen die Übereinstimmung aller Seitenlängen und aller Winkel beider Dreiecke.
Seite-Seite-Seite
Alle drei Seitenlängen der beiden Dreiecke stimmen überein.
Seite-Winkel-Seite
Zwei Seiten beider Dreiecke haben dieselbe Länge, und der von beiden Seiten eingeschlossene Winkel stimmt überein.
Winkel-Seite-Winkel
Eine Seitenlänge beider Dreiecke hat dieselbe Länge, und die an der gleich langen Seite anliegenden Winkel beider Dreiecke sind gleich groß.
Seite-Seite-Winkel
Zwei Seiten beider Dreiecke stimmen überein, sowie der Winkel der der längeren Seite gegenüberliegt.
